Integraal
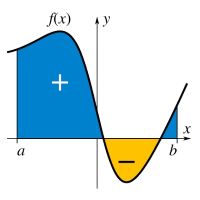
De bepaalde integraal is het oppervlak begrensd door de grafiek van een functie f(x) tussen twee punten a en b. Het is gebruikelijk om oppervlakken boven de x-as (blauw) positief en oppervlakken onder de x-as (geel) negatief te rekenen (zie figuur).
b
∫ f ′(x) dx = f(b) - f(a)
a
waar f ′(x) de afgeleide is van de functie f(x). Enkele voorbeelden zijn:
| f ′(x) | f(x) | |
|---|---|---|
| c | c x | |
| xc (c ≠ -1) | (c+1)-1 xc+1 | |
| x-1 | ln(|x|) | |
| ec x | c-1 ec x | |
| sin(c x) | -c-1 cos(c x) | |
| cos(c x) | c-1 sin(c x) |
Gerelateerde eenheden
Laatst gewijzigd:31 december 2025 17:01
View this page in: English
