De massa van de zon? Simpel!
Voor onderhoudende experimenten heb je niet per se een groot laboratorium nodig. Een paar formules en een rekenmachine en voilà, je berekent de massa van de zon. En dat had je nu altijd al eens willen doen.
Eén op de vier Nederlanders denkt dat de zon om de aarde draait. Serieus waar: één op de vier. Dat bleek een paar jaar geleden uit een quiz van de Europese Commissie, bedoeld om de wetenschapskennis van Europeanen te testen. Gelukkig doet Nederland het net iets beter dan het Europees gemiddelde. Eén op de drie Europeanen denkt dat de aarde het middelpunt van het heelal is. Op het gevaar af dat ik in herhaling verval: serieus waar. Eén op drie.
Van de mensen die wél weten hoe het zit met de zon en de aarde en de maan, heeft nog eens één op de drie geen flauw benul hoe lang de aarde nodig heeft voor een rondje om de zon. Een dag? Een maand? Geen idee eigenlijk. Om het nog even erger te maken: de Europese quiz bestond uitsluitend uit multiple–choicevragen.
Voor wie het kwijt was: de aarde draait in een jaar om de zon. Of, om heel precies te zijn, in 365,25636 dagen. Als je weet hoe lang de aarde erover doet om rond de zon te cirkelen, ben je nog maar drie stappen verwijderd van de massa van de zon.
Je hebt nog twee getallen nodig: de gemiddelde afstand van de aarde tot de zon (149.597.870,7 kilometer) en Newtons universele gravitatieconstante G – ook wel aangeduid als de ‘Big G’, ter onderscheid van de ‘Small g’, die staat voor de zwaartekrachtsversnelling.
De formule voor massa van de zon is eigenlijk vrij simpel: Mzon = (v2r)/G, waarin v de omloopsnelheid van de aarde is in meters per seconde, r de straal van de aardbaan en G de universele gravitatieconstante: 6,67 × 10-11m3kgs2.
De snelheid (29.784 meter per seconde) kun je berekenen door de omtrek van de aardbaan uit te rekenen (2πr) en vervolgens te delen door de omlooptijd (365,25636 dagen = 31558149,504 seconden). Vul alle getallen in op de juiste plaats in de formule en wat krijg je? 1.989.599.323.298.101.907.046.476.761 kilo en 619 gram.
En omdat we nou toch bezig zijn: je kunt met hetzelfde gemak de massa van de aarde uitrekenen aan de hand van de omloopsnelheid (1023 meter per seconde) en de afstand (3,844 × 108 meter) van de maan: 5.895.670.164.917.541.229.385 kilo en 307 gram.
Kun je, om de hattrick compleet te maken ook de massa van de maan uitrekenen? Het probleem is een beetje dat de rekensom maar één kant op werkt. Uit de omlooptijd van de maan kun je wel de massa van de aarde berekenen, maar niet de massa van de maan. Net zozeer als je uit de baan van een kunstmaan niet z’n massa kunt bepalen. Volgens overlevering zou president Eisenhower in een crisisberaad na de lancering van de Sputnik hebben gevraagd of zijn generaals “op basis van z’n baan” konden berekenen hoe zwaar de Sovjetkunstmaan was. Nee dus, maar op basis van de afstand en omloopsnelheid konden ze de president wel precies vertellen hoe zwaar de aarde was. Het is niet bekend of de generaals dat ook voorgerekend hebben. En of de president het wilde weten.
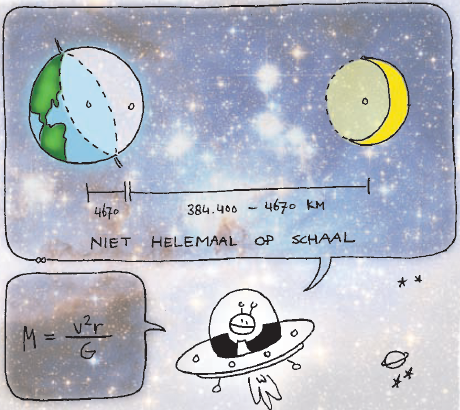
Hoe bereken je dan de massa van de maan? Daarvoor moet je weten dat de maan niet om de aarde draait, maar dat de aarde en de maan om een gemeenschappelijk middelpunt draaien. Dat gemeenschappelijke zwaartepunt ligt ongeveer 4670 kilometer van het middelpunt van de aarde. De rest is een invuloefening: de afstand van het middelpunt van de aarde tot zwaartepunt keer de aardmassa is gelijk aan de afstand van het zwaartepunt tot de maan keer de massa van de maan. Drie van die vier getallen heb je al. Vermenigvuldig het gewicht van de aarde met 4670/(384400-4670) en kijk: 72.506.195.674.560.719.640 kilo. En 180 gram.
Auteur: Ernst Arbouw
| Laatst gewijzigd: | 12 april 2021 13:11 |

